アルゴリズムとデータ構造―基本情報など情報処理試験対策用の解説
トップ 情報処理の知識体系
情報処理の知識体系 テクノロジ系
テクノロジ系 基礎理論
基礎理論 アルゴリズムとプログラミング
アルゴリズムとプログラミング アルゴリズムとデータ構造
アルゴリズムとデータ構造
アルゴリズムとデータ構造について、基本情報や応用情報など情報処理試験対策用の解説をまとめています。
目次
このページの目次です。
1. データ構造
データ構造の考え方などデータ構造とは何か、まとめていきます。
データ構造とは
データ構造とは、コンピュータがデータ処理や計算を行う際に、あらかじめデータを扱いやすいように加工しておき、 計算速度が速くなるようにしたものです。
データ構造の種類
データ構造の種類についてまとめていきます。
配列
配列の考え方を理解し、データの格納方法,取出し方法などの操作を見ていきます。
配列とは
配列とは、内部構造を持つデータ構造で、同じ型の要素の並びで添字式を持つデータ構造のことをいいます。
配列(数値)要素の並べ替えの例
配列の例として、数値の配列の要素の並べ替えについて見ていきます。 以下ではグループ内では、処理がおこなわれた数値を左から順に並べるものとして、手順に従って6個の数値の配列「180、315、282、410、645、525」を並べ替えます。
手順
| 手順1 | 並びの左から順に、数値の1の位の値によって0~9のグループに分ける。 |
| 手順2 | 次に0のグループの数値を左側から順に取り出して並べ、その右側に1のグループ、以下順に2~9のグループの数値を並べていく。 |
| 手順3 | 手順2で得られた数値の並びの左側から順に、数値の10の位によって0~9のグループに分ける。 |
| 手順4 | 手順2と同様に、0のグループの数値から順に並べる。 |
手順1
並べの左側から順に、数値の1の位の値によって0~9のグループに分けます。
| 1の位が0のグループ | 180、410 |
| 1の位が1のグループ | |
| 1の位が2のグループ | 282 |
| 1の位が3のグループ | |
| 1の位が4のグループ | |
| 1の位が5のグループ | 315、645、525 |
手順2
0のグループの数値を左側から順に取り出して並べ、その右側に1のグループ以下順に2~9のグループの数値を並べて行きます。
180、410、282、315、645、525
となります。
手順3
| 10の位が0のグループ | |
| 10の位が1のグループ | 410、315 |
| 10の位が2のグループ | 525 |
| 10の位が3のグループ | |
| 10の位が4のグループ | |
| 10の位が5のグループ | |
| 10の位が6のグループ | 645 |
| 10の位が7のグループ | |
| 10の位が8のグループ | 180、282 |
| 10の位が9のグループ |
手順4
手順2と同様に、0のグループの数値から順に並べます。
410、315、525、645、180、282
配列に関連したIPA情報処理試験の過去問題
以下では配列に関連したIPA情報処理試験の過去問とその解説をまとめています。
リスト
リストの考え方,その操作を理解します。
スタックとキュー
スタックはLIFO(Last-In First-Out:後入れ先出し)、キューはFIFO(先入れ先だし:First In First Out)のデータ構造です。 スタックとキューの考え方、その操作について解説していきます。
木構造
木は、要素同士の階層関係を表現するための問題向きデータ構造です。 詳細で、木構造の種類についてまとめています。根、葉、枝などの用語のやさしい説明から、順序木、2分木、多分木、b木、b+木、バランス木などの考え方やイメージ、計算量、ヒープ、幅優先探索など、情報処理の過去問と合わせてまとめました。
2. アルゴリズム
アルゴリズムとは何かの意味から、代表的なアルゴリズムについてまとめています。
ITにおけるアルゴリズムとは
ITやコンピューター分野におけるアルゴリズムは、コンピュータで問題を処理するためにプログラムとして表現するのに向いている解決法です。 例をあげると、グラフ理論、オペレーションズリサーチ、数値計算、データ構造の操作、整列、数式処理、言語処理などです。
参考)アルゴリズムとは
アルゴリズムとは、一般的には算法と訳されます。一般的な意味、ITや医療などで使われるアルゴリズムの意味をまとめています。
流れ図
流れ図とは、フローチャートともいわれ、データの流れや問題解決の手順(アリゴリズム)を表す図のことをいいます。
有名なアルゴリズムにユークリッドの互除法がありますが、以下はその流れ図の例になります。 ユークリッド互除法は、2つの整数の割算を繰り返して最大公約数を求める方法です。
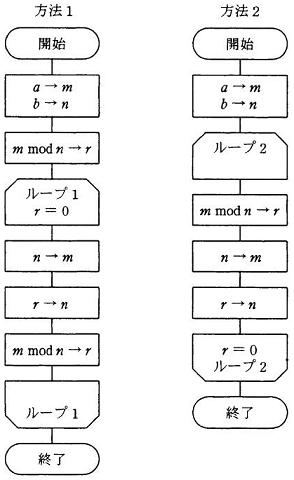
流れ図に関連したIPA情報処理試験の過去問題
以下では流れ図に関連したIPA情報処理試験の過去問とその解説をまとめています。
代表的なアルゴリズム
代表的なアルゴリズムを修得し、応用できるようにしていきます。
整列・併合・探索のアルゴリズム
整列のアルゴリズム、併合のアルゴリズム、探索のアルゴリズムを理解していきます。
挿入ソート
挿入ソートは、単純挿入整列法とも呼ばれ、整列済みの要素と追加する要素を比較し ながら適切な場所に挿入するアルゴリズムです。
挿入ソートの例
文章で説明するより、例を見た方が分かりやすいです。
挿入ソート(単純挿入整列法)で昇順に並べる例)
[2][4][1][3]
⇒ [2][4][1][3] ・・・ [2]と[4]を比較、[2]の方が小さいのでそのまま
⇒ [2][1][4][3] ・・・ [4]と[1]を比較、[4]の方が大きいので入れ替え
⇒ [1][2][4][3] ・・・ [2]と[1]を比較、[2]の方が大きいので入れ替え
⇒ [1][2][4][3] ・・・ [2]と[4]を比較、[2]の方が小さいのでそのまま
⇒ [1][2][3][4] ・・・ [4]と[3]を比較、[4]の方が大きいので入れ替え
挿入ソートのオーダー
整列済みのものを整列するので入れ替えが発生しないため、n-1回の比較で整列が完了します。 なので、オーダー的にはnとなります。
挿入ソートに関連したIPA情報処理試験の過去問題
以下では挿入ソートに関連したIPA情報処理試験の過去問とその解説をまとめています。
クイックソート
クイックソートは以下のように並べ替えを行うソート方法です。
①適当な基準値を選び、それよりも小さな値のグループと大きな値のグループにデータを分割する。
②同様にして、グループの中で基準値を選び、それぞれのグループを分割する。
①②の操作を繰り返していく方法です。
クイックソートに関連したIPA情報処理試験の過去問題
以下ではクイックソートに関連したIPA情報処理試験の過去問とその解説をまとめています。
ヒープソート
ヒープソートでは、木構造を配列で表現するデータ構造を利用したソートアルゴリズムで、利用する木構造は半順序木とよばれる順序木を使用します。 未整列の部分を順序木にし、そこから最小値を取り出して整列済の部分に移します。 この操作を繰り返して、未整列の部分を縮めていきます。
ヒープソートに関連したIPA情報処理試験の過去問題
以下ではヒープソートに関連したIPA情報処理試験の過去問とその解説をまとめています。
線形探索法
線形探索法は、先頭のデータから順に目的のデータがあるかを比較していく探索法です。 最短で1回、最長でn回、平均で(1+n)/2回の探索が行われます。
線形探索法に関連したIPA情報処理試験の過去問題
以下では線形探索法に関連したIPA情報処理試験の過去問とその解説をまとめています。
2分探索
2分探索とは、探索データの中央の値と目的のデータを比較し、一致しなければ、中央の値の上下どちらにあるかを判断し、探索データを半分に絞り込み、比較を続けていく方法です。 探索されるデータが昇順、または降順に整列している場合に使用できます。
2分探索に関連したIPA情報処理試験の過去問題
以下では2分探索に関連したIPA情報処理試験の過去問とその解説をまとめています。
ハッシュ表探索法
ハッシュ表探索法は、ハッシュ表を使用したデータを高速に検索するための方法の1つです。
再帰のアルゴリズム
再帰的アルゴリズムは、関数の定義中にその関数自身への参照が定義中に表れるアルゴリズムです。
再帰的アルゴリズムの例
再帰的アルゴリズムの例としては、n!や自然数の定義、木構造の探索、クリックソート、マージソートのアルゴリズムなどがあります。
再帰のアルゴリズムに関連したIPA情報処理試験の過去問題
以下では再帰のアルゴリズムに関連したIPA情報処理試験の過去問とその解説をまとめています。
もっと知識を広げるための参考
-
テクノロジ系
情報処理試験対策用のサイトオリジナル教科書をテーマにテクノロジ系の知識をまとめています。
更新履歴
- 2018/12/18 クイックソートについて追記しました。
- 2018/11/19 スタックからのデータの取り出し方について追記しました。
- 2018/9/23 スタックの応用例について補足を追記しました。
- 2018/7/7 スタックの例を追記しました。
- 2017/5/31 配列(数値)要素の並べ替えの例、2分探査法について追記しました。
- 2017/3/31 ユークリッドの互除法について追記しました。
- 2017/3/30 木に関する用語説明、 挿入ソート(単純挿入整列法)、線形探索法、再帰のアルゴリズムについて追記しました。
- 2017/1/8 ヒープおよびヒープソートについて追記しました。