木構造―種類のやさしい説明、多分木、b木、b+木、幅優先探索など

トップ情報処理の知識体系テクノロジ系基礎理論アルゴリズムとプログラミングアルゴリズムとデータ構造データ構造の種類 木構造

木構造の種類についてまとめています。根、葉、枝などの用語のやさしい説明から、順序木、2分木、多分木、b木、b+木、バランス木などの考え方やイメージ、計算量、ヒープ、幅優先探索など、情報処理の過去問と合わせてまとめました。

▲記事トップへ

1. 木構造とは

木構造とは、グラフ理論という数学の1分野の木の構造をしたデータ構造のことをいいます。英語で「tree structure」とつづります。木構造のことを単に「木」と呼ぶこともあります。

2. 木構造に関する用語

木に関する用語を見ていきます。

節　…木構造を図示した場合のノード部分のことをいいます。
枝　…各節の上下関係のことをいいます。
親　…上位の節のことをいいます。
子　…下位の節を子といいます。
根　…最上位の節のことをいいます。
葉　…最下位の節のことをいいます。

3. 木構造の種類

子ノード数での分類した2分木と多分木、すべての葉について、深さがほぼ等しいバランス木、ヒープ、デジタル木など多数の分類方法があります。以降の章で、順序木、2分木、多分木、b木、b+木、バランス木、ヒープなどの木構造の種類をまとめています。

4. 多分木

多分木とは、兄弟の数がn以上である順序木のことをいいます。

順序木

節にデータを格納するとき、一定の順序で格納してある木を順序木といいます。

2分木

葉以外の節が2つまたはそれ以下の子を持つような順序木を2分木といいます。

節が持つこの数で順序木の種類を分類するとき、この最大数をkとすると、2分木はk=2、一般的にk≧2の場合、多分木といいます。

5. B木

B木とは、木構造をもつデータ構造の1つで、多分木を基にしたバランス木です。節を複数持つことができる木構造で、階層の深さが同じになるように、ノードの分割と併合を行います。

B木はバランス多分木ともいい、枝が複数ある木構造のうち、根からすべての葉の深さが同じで、枝が一方向に偏らないような構造の木のことをいいます。

B木の条件

B木は、次のような制約を持ちます。

根以外はk個以上の要素を持つ
各節には最大で2k個の要素が含まれる
各節は要素数に1を加えた数の子を持つ
根からすべての葉までの深さは等しい

B木のイメージ

以下はB木のイメージです。各節点に4個のキーを格納し、5本の枝を出し、根の深さがレベル2まであるB木になります。このB木には、レベル0がキー4個、レベル1がキー20個、レベル2がキー100個、合計124個のキーが格納されています。

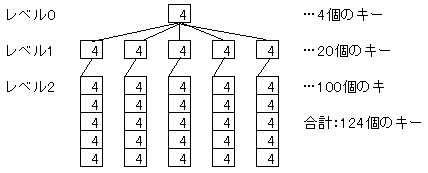
B木の応用例

B木は、階層型データベースなどで利用されるデータ構造です。

補足

バランス木について補足です。

バランス木

バランス木とは、節の追加や削除が発生するごとに、木構造全体を再調整する機能を持つ木です。特定の部分木だけが伸びることを防ぐために、バランス木の各部分木は左と右の深さの情報を持っています。

6. B+木

B+木は、B木から派生したB木の変種でキーを指定することで挿入・検索・削除が効率的に行える木構造の一種です。

B+木インデックスを格納するノードへのアクセス回数のオーダ

B+木インデックスのが定義されている候補キーを利用して、1件のデータを検索するとき、データ総件数Xに対するB+木インデックスを格納するノードへのアクセス回数のオーダを表す式はlogXです。

1つの接点にm個の枝があるB+木があるとします。根から順に範囲を狭めながら探索していきますが、B+木のバランスの取れた木ですので、深さが1つ深まると探索対象が1／mに減ることが見積れます。最終的に探索範囲が1、つまり「X／mのt乗＝1」となるまで探索するのが最悪の探索回数となります。

これをtの式に直すと、「t＝logmX」となります。オーダーで考える場合には、対数の底は考える必要ないのでlogXとなります。

7. ヒープ

データ構造やヒープ領域とは何かなど、ヒープをテーマに情報をまとめています。

詳細

8. 幅優先探索

木の節をなぞることを木の探索あるいは走査、巡回といいます。なぞり方を大きく分類すると、幅優先探索と深さ優先探索に分けられます。ここでは幅優先探索について見ていきます。

幅優先探索とは

幅優先探索とは、木構造の始点から近い順に1つずつ調べていく探索法のことをいいます。

幅優先探索のなぞり方

幅優先探索のなぞり方は、木のレベル0から始めて、同じレベルの左から右になぞり、右端まで来たら下のレベルに移って、同じようになぞります。

木構造に関連したIPA情報処理試験の過去問題

以下では木構造に関連したIPA情報処理試験の過去問とその解説をまとめています。

もっと知識を広げるための参考

アルゴリズムとデータ構造
基本情報など情報処理試験対策用の解説。このページではアルゴリズムとデータ構造について解説しています。
テクノロジ系
情報処理試験対策用のサイトオリジナル教科書をテーマにテクノロジ系の知識をまとめています。

更新履歴

2018年07月15日記事を作成しました。

戻る

スポンサーリンク

情報処理の知識体系

各試験の問題と解説

ランダム出題・採点アプリ

プログラミング