離散数学―離散数学とは?離散数学の入門知識を整理。問題もあり
トップ 情報処理の知識体系
情報処理の知識体系 テクノロジ系
テクノロジ系 基礎理論
基礎理論 離散数学
離散数学
離散数学とは何か、入門知識をまとめています。情報処理試験の過去問から抜粋した問題も示しています。
基数、基数の変換、数値の表現、算術演算と精度など、コンピュータで扱う数値表現を修得し、応用すること。 また、集合、論理演算の基本法則、手法を修得し、応用することを目標に入門知識をまとめていきます。
加えて、情報処理試験の過去問から抜粋して問題も示していきます。
目次
この記事の目次です。
1. 離散数学とは
2. 基数
3. 数値の表現
4. 算術演算と精度
5. 集合と命題
6. 論理演算
1. 離散数学とは
離散数学とは、連続でない、とびとびの対象をあつかう数学のことです。
離散数学の分野
離散数学は、情報科学の様々な分野で、それぞれに理論的基礎を構成しています。 数論などとても古い分野やブール代数、オートマトン、計算論、符号論など、近世・近代に花開いた新しい分野があります。 以前まで「情報数学」とうい名前のもとに包含されていました。
離散数学とはに関連した参考書籍
離散数学とはに関連した参考書籍です。目次や参考いたしました内容をまとめています。
- Amazon)はじめての離散数学
2. 基数
基数とは何かと2進数、8進数、10進数、16進数、n進数の表現、2進数と10進数などの基数の変換手法、関連する情報処理試験の問題をまとめています。
3. 数値の表現
表現可能な数値の範囲、負の数の表現(補数表現)、小数の表現など数値の表現について触れていきます。
電話番号の表現
次の体系をもつ電話番号で、80憶個の番号を創出したいとすると番号の最低限必要な桁数は幾つになるでしょうか。 桁数には“020”を含むという条件があります。
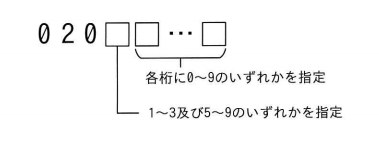
先頭は020固定で、次に来るのは1~3と5~9の8種類あり、残りの桁で10億パターン創出する必要があります。 10億は「1,000,000,000」、つまり残り9桁になり、3+1+9=13、必要な桁数は13桁になります。
負の数の表現(補数表現)
コンピュータでは、負数を表現するときに補数を用いるのが一般的です。負の数の表現(補数表現)について見ていきます。
補数
補数とは、与えられた数を決められた数から引くことによって得られる数のことをいいます。
n進数の場合、基数の補数であるnの補数と基数から1引いた補数であるn-1の補数があります。
負数を2の補数で表現する固定小数点表示法
負数を2の補数で表現する固定小数点表示法において、nビットで表現できる範囲は、
ー2n-1~2n-1ー1
となります。
小数の表現
小数の表現について見ていきます。
浮動小数点数
浮動小数点数は、非常に大きな数や非常に小さな数を扱う場合に使用します。 浮動小数点数の構成は次のようになっています。

図 浮動小数点数の構成
たとえば0.000000000000000101×23という数値では、仮数部のけたが不足して表現できなくなってしまいます。
そこで、指数部を調整することで仮数部の左側の0をシフトして消していきます。 このように仮数部を調整することで仮数部の左側の0を消して、より大きな数値やより小さな数値を表現できるようにする作業を正規化といいます。
正規化の例
ここでは10進数0.25を正規化した表現を考えます。
まず10進数0.25を2進数に基数変換します。
(0.25)10 = (0.01)2
次に2進数0.01を正規化します。
(0.01)2 = (0.1)2×2-1
よって仮数部は、(10000000000)2
指数部は2を基数とし、負数は2の補数で表現します。
また、-1を2の補数で表現します。
(1111)2 = (-1)10
したがって、
S:仮数部の符号は正なので、0となります。
e:指数部は(1111)2です。
f:仮数部は(10000000000)2です。
BCD(Binary Coded Decimal:2 進化 10 進)
BCDとは、Binary Coded Decimalの略で、十進法の1桁を、0から9までを表す2進数の4桁で表す(コンピュータにおける)数値の表現方式です。
数値の表現に関連したIPA情報処理試験の過去問題
以下では数値の表現に関連したIPA情報処理試験の過去問とその解説をまとめています。
- 令和元年秋 問82 必要な桁数―ITパスポート
- 平成18年春 問3 負数を2の補数で表現する固定小数点表示法―基本情報技術者 午前
- 平成18年春 問4 10進数0.25を正規化した表現―基本情報技術者 午前
4. 算術演算と精度
加減乗除、表現可能な数値の範囲、シフト演算、演算精度(誤差とその対策)など、コンピュータでの算術演算について見ていきます。
シフト演算
コンピュータは、シフト演算という方法で掛け算を行います。 シフト演算は、データのビットの並びを左右に何ケタかずらす演算です。
論理シフト演算
論理シフト演算とは、データを数値として扱うのではなく、単にビットの並びとして扱うときに使われます。
図は、8ビットのデータを左に2ビット論理シフトする例です。 左に2ビット論理シフトした結果、あふれた2ビットはそのまま捨てられます。 また、空いた左側の2ビットは0で埋められます。
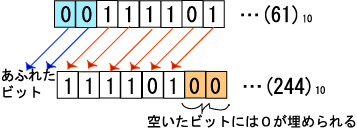
正の数値を扱うだけであれば、論理シフトで掛け算と割り算が行えます。 2倍、4倍、8倍、…や2分の1、4分の1、8分の1、…を行う2進数の乗算や除算は、論理シフトで実現できます。 ただし、論理シフトでは負の数値を扱うことは出来ません。
演算精度(誤差とその対策)
誤差には、桁落ち誤差、情報落ち誤差、などの誤差があります。誤差について見ていきます。
けた落ち
はけた落ちとは値がほぼ等しい二つの数値の差を求めたとき、有効桁数が減ることによって発生する誤差です。 英語で「cancellation of significant digits」と書きます。
絶対値のほぼ等しい数値の差を求める場合、正規化によって、有効桁数が減少してしまう現象をけた落ちといいます。
丸め誤差
丸め誤差とは、指定された有効桁数で演算結果を表すために、切り捨て、切り上げ、四捨五入などで下位の桁を削除することによって発生する誤差です。 英語で「rounding error」あるいは「round-off error」と書きます。
情報落ち
情報落ちとは、絶対値の非常に大きな数値と小さな数値の足し算や引き算を行ったとき、小さな数値が計算結果に反映されないことによって発生する誤差です。
浮動小数点表示では、指数部と仮数部に分けて計算します。 例えば1234(10は0.1234×10の4乗と表せます。
桁落ちは減算により有効数字が少なくなる際に発生する誤差で、情報落ちは加算により小さい方の仮数部の下位桁情報が失われる際の誤差です。
情報落ちの例
例としては、浮動小数点表示の仮数部が23ビットであるコンピュータで計算した場合、次の計算式は情報落ちします。
(1.01)2×218+(1.001)2×2-5
このようなことより、浮動小数点表現を使った足し算や引き算を行う場合、指数をそろえる必要があります。 絶対値が非常に大きい数と絶対値が非常に小さい数を使って足し算や引き算を行うと、どちらかの指数にあわせるため仮数部のけたが入りきれなくなり、小さい数が計算に反映されないことがあります。
打ち切り誤差
打ち切り誤差とは、無限級数で表される数値の計算処理を有限項で打ち切ったことによって発生する誤差です。
算術演算と精度に関連したIPA情報処理試験の過去問題
以下では算術演算と精度に関連したIPA情報処理試験の過去問とその解説をまとめています。
5. 集合と命題
集合、命題、ベン図の手法と考え方についてまとめていきます。
集合
集合とは、関心を払っているものの集まりで、次の2つの性質を持っているものです。
- ある対象がその集合に属するかどうか明確に判断できること
- 集合に属するある2つの対象が同一のものかどうか知り得ること
集合表記の意味
集合表記の意味、X∪YはXとYの和集合つまり「または」、X∩YはXとYの積集合つまり「かつ」、
ベン図による集合の演算の表現
集合の間の演算は図のようなベン図を用いて表現するとわかりやすいことがあります。
X∪YはXとYの和集合、X∩YはXとYの積集合、
集合と命題に関連したIPA情報処理試験の過去問題
以下では集合と命題に関連したIPA情報処理試験の過去問とその解説をまとめています。
6. 論理演算
論理式の表現、論理演算、ド・モルガンの法則などの基本法則、真理値表、カルノー図の手法をまとめていきます。
カルノー図
カルノ―図とは論理式を簡単化する図。カルノ―図による論理式を導くやり方を例題付きで解説。情報処理試験の過去問を練習問題(解答付き)としてまとめています。
真理値表
論理式からの真理値表の書き方、論理回路からの真理値表の書き方など。真理値表についてまとめています。
もっと知識を広げるための参考
以下は、もっと知識を広げるため参考ページです。知識を広げる参考になればと思います。
テクノロジ系
情報処理試験対策用のサイトオリジナル教科書をテーマにテクノロジ系の知識をまとめています。
更新履歴
- 2021/10/26 BCDについて追記しました。
- 2020/12/31 電話番号の表現について追記しました。
- 2018/5/27 丸め、打切りの誤差の説明について追記しました。
- 2017/11/18 離散数学とはに関連した参考書籍について追記しました。
- 2017/5/31 シフト演算について追記しました。
- 2017/5/29 補数、集合について追記しました。
- 2017/3/25 誤差について追記しました。