真理値表―論理回路からの真理値表の書き方
トップ
情報処理の知識体系
テクノロジ系
基礎理論
離散数学
論理演算
真理値表
論理式からの真理値表の書き方、論理回路からの真理値表の書き方など。真理値表についてまとめています。
目次
この記事の目次です。
1. 真理値表とは
2. 論理式とは
3. 論理回路とは
4. 論理式と等価な論理回路を求める例
5. 真理値表の例
6. 論理回路からの真理値表の書き方の例
7. 真理値表の作り方の参考情報
8. 真理値表に関連したIPA情報処理試験の過去問題
1. 真理値表とは
真理値表とは、真理値を一覧表に表したもののことです。
論理式から論理回路を求めたり、論理回路の演算結果を求める際に真理値表を活用すると便利です。
論理学では「真理表」とも呼ばれる
「真理値表」は論理学のテキストによっては「真理表」とも呼ばれています。「真理値表」はその他に「真偽表」などの呼び方もあります。
真理値
真理値とは、命題のうち、正しいと判断できいることを真（True）、誤っていると判断できることを偽（False）、真偽を総称して真理値といいます。
2. 論理式とは
論理式とは、論理記号を用いていくつかの命題を結び合わせた式のことをいいます。
3. 論理回路とは
論理回路とは、英語でlogic circuitといい、論理演算を行うコンピューターなどの電気回路のことをいいます。
論理回路の種類
論理回路の種類には、以下のようなものがあります。
- 論理積（AND）：
- 論理和（OR）：
- 否定論理積（NAND）：
- 否定論理和（NOR）：
4. 真理値表の例
簡単な真理値表の例です。
NOR回路の真理値表
NOR回路（A NOR B）の真理値表です。
| A | B | A NOR B |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
5. 論理式と等価な論理回路を求める例
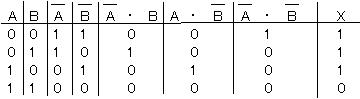
例えば、論理式X＝A・B＋A・B＋A・Bという論理式と等価な論理回路を求める場合、真理値表を作成すると以下のようになります。 論理式AとBの否定論理積と等しいことがわかります。
6. 論理回路からの真理値表の書き方の例
真理値表の書き方を示すため、以下の論理回路から真理値表を作成します。
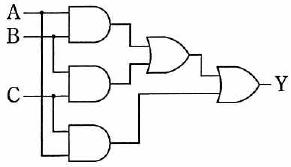
真理値表は以下になります。
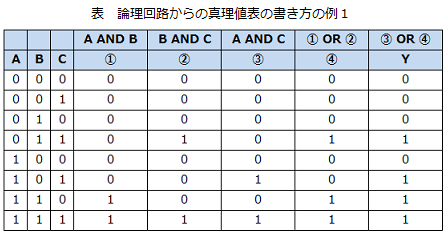
7. 真理値表の作り方の参考情報
真理値表を作る際の参考になります。
Excelで真理値表を作る際に使える関数
Excelで真理値表を作る場合、or関数「A+B は or(A, B)」、not関数「A^ はnot(A)」、and関数「A•Bは and(A, B)」といった関数が使えます。
論理式に使われる記号の意味
論理式に使われる記号は同じ意味でも流派などによって異なる記号が使われています。 論理式に使われる記号の意味を対応表に整理してみました。
| 意味 | 使用される記号 |
|---|---|
| 実質含意（含む、もし〜ならば） | ⇒、→、⊃ |
| 実質等値（〜のとき、かつそのときに限り） | ⇔、≡、↔ |
| 否定（〜ではない） | ¬、˜、! |
| 論理積（かつ、and） | ∧、· 、＆ |
| 論理和（または、or） | ∨、+、∥ |
| 排他的論理和（xor） | ⊕、⊻ |
| トートロジー （トップ） | ⊤、T、1 |
| 矛盾（ボトム） | ⊥、F、0 |
| 全称量化（すべての、任意の、それぞれについて ） | ∀ |
| 存在量化（〜が存在する） | ∃ |
| 唯一存在量化（〜がただ1つ存在する ） | ∃! |
| 定義（〜として定義される） | ≔、≡、:⇔ |
| 優先順位（括弧） | ( ) |
| ターンスタイル（〜を証明する ） | ⊢ |
| ダブル・ターンスタイル（〜を含意する） | ⊨ |
8. 真理値表に関連したIPA情報処理試験の過去問題
真理値表に関連したIPA情報処理試験の過去問題です。
もっと知識を広げるための参考
-
離散数学
離散数学とは何か、入門知識をまとめています。情報処理試験の過去問から抜粋した問題も示しています。
更新履歴
- 2021/9/7 NOR回路の真理値表について追記しました。
- 2021/7/12 真理値表の作り方の参考情報について追記しました。
- 2017/5/16 論理式と等価な論理回路を求める例について追記しました。