カルノー図とは―説明、やり方、練習問題（解答付き）。

トップ情報処理の知識体系テクノロジ系基礎理論離散数学論理演算 カルノー図

カルノー図とは論理式を簡単化する図。カルノー図による論理式を導くやり方を例題付きで解説。情報処理試験の過去問を練習問題（解答付き）としてまとめています。

▲記事トップへ

1. カルノ―図とは

カルノ―図とは、複雑な論理式を簡単に表記することを目的とした図です。論理演算中の項を簡単化しやすくする図です。英語で「Karnaugh map」です。

ベンチ図

カルノー図に似た図としてベンチ図があります。ベンチ図はカルノー図の変数と数字の書き方が異なります。

2. カルノ―図の例題とやり方

例題として、カルノ―図から論理式を導くやり方を解説していきます。以下のA、B、C、Dを論理変数とするカルノー図と等価な論理式を導くやり方を示していきます。なお、・は論理積、＋は論理和、XはXの否定を表します。

A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D

書き方（作り方）

まずは、カルノー図を作ります。

カルノー図の書き方は、たとえば、3変数の場合はA/BCで縦に0と1、横に00、01、11、10を並べた表を書きます。 4変数の場合はAB/CDのように縦と横にマークする項目を決めて、クロス表を埋めていきます。

以下は4変数の論理式のカルノー図の例です。

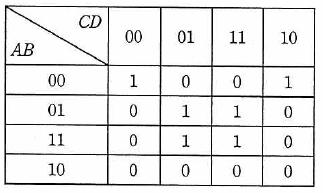
カルノー図では表の00、01、10、11という順番ではなく、00、01、11、10の順番で書き、以下のように論理和（＋）で分割した論理式をクロス表に真理値を入れていきます。

A・B・C・D　⇒　AB=00、CD=00
A・B・C・D　⇒　AB=00、CD=10
A・B・C・D　⇒　AB=01、CD=01
A・B・C・D　⇒　AB=01、CD=11
A・B・C・D　⇒　AB=11、CD=01
A・B・C・D　⇒　AB=11、CD=11

解き方

例のカルノ―図を以下の手順に従って、簡単かした論理式が導きだます。

1が記入されている部分をグループ化
グループ化した部分を論理式で表す
グループ内の共通項の論理積を抽出する
グループの共通項をまとめた論理積の式を結合して和の式にする

解き方1）1が記入されている部分をグループ化

以下のように赤枠の部分と青枠の部分がグループ化できます。

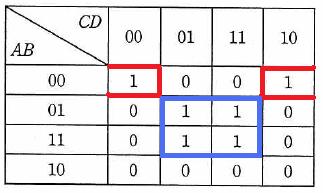
解き方2）グループ化した部分を論理式で表す

赤枠の部分を論理積であらわすと以下になります。

AB=00、CD=00　⇒　A・B・C・D
AB=00、CD=10　⇒　A・B・C・D

青枠の部分を論理積であらわすと以下になります。

AB=01、CD=01　⇒　A・B・C・D
AB=01、CD=11　⇒　A・B・C・D
AB=11、CD=01　⇒　A・B・C・D
AB=11、CD=11　⇒　A・B・C・D

解き方3）グループ内の共通項の論理積を抽出する

赤枠の部分を共通項の論理積はA・B・Dになります。

AB=00、CD=00　⇒　A・B・C・D
AB=00、CD=10　⇒　A・B・C・D

青枠の部分を共通項の論理積はB・Dになります。

AB=01、CD=01　⇒　A・B・C・D
AB=01、CD=11　⇒　A・B・C・D
AB=11、CD=01　⇒　A・B・C・D
AB=11、CD=11　⇒　A・B・C・D

解き方4）グループの共通項をまとめた論理積の式を結合して和の式にする

グループの共通項をまとめた論理積の式を結合して和の式にするとカルノ―図と等価な論理式になります。

A・B・D＋B・D

論理式の簡単かの結果

以上より、

A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D ＋ A・B・C・D

という論理式は、以下のように簡単かされました。

A・B・D＋B・D

3. カルノ―図の練習問題（解答付き）

カルノ―図に関連したIPA情報処理試験の過去問です。練習問題として参考にしてください。解答付きです。

平成26年秋問1 カルノ―図―情報処理試験（高度共通）

もっと知識を広げるための参考

離散数学
離散数学とは何か、入門知識をまとめています。情報処理試験の過去問から抜粋した問題も示しています。

更新履歴

2021/8/17 書き方（作り方）について追記しました。
2016/10/10 記事をUPしました。

戻る

スポンサーリンク

情報処理の知識体系

各試験の問題と解説

ランダム出題・採点アプリ

プログラミング