基礎数学

トップ 情報処理の知識体系 テクノロジ系 基礎理論 基礎数学

中学と高校で習う数学（基礎数学）についてまとめています。

▲記事トップへ

目次

この記事の目次になります。

1. 数と式
2. 方程式
3. 関数とグラフ
4. 平面図形
5. 空間図形
6. データの活用

もっと知識を広げるための参考
更新履歴

1. 数と式

数と式についてまとめていきます。

整数・自然数

0と、0から1ずつ足されて得られる数、0から1ずつ引いて得られる数を整数といいます。 0をふくまない1以上の整数、つまり正の整数を自然数といいます。

小数

1.5、0.76のような数を小数といい、「.」を小数点といいます。

分数

分数は、整数を0でない整数で割った形で表した数です。

詳細

正の数・負の数

小学校の算数では0と正の数だけ、中学校になると数の範囲が負の数まで広がります。 負の数の意味を理解して、負の数をふくむ数の計算になれましょう。

詳細

加法と減法

足し算のことを加法といいます。二つの数に対してそれを加え合わせて第三の数を求めます。 減法は引き算で、二つの数に対して一方の数から他方の数を引き去った第三の数を求めることをいいます。

和と差

加法の結果を和、減法の結果を差といいます。

加法

加法は、同符号の2数の和の場合は、絶対値の和になり、共通の符号をつけます。 異符号の2数の和の場合は、絶対値の差になり、絶対値の大きいほうの符号をつけます。

例1）(-2)+(-3) = -(2+3) = -5

例2）(-3)+(+5) = +(5-3) = +2

例3）(+2) + (-3) = -(3 - 2) = -1

項

加法だけの式に直したとき、加法の記号＋で結ばれる各数を項といいます。

減法、3つ以上の数の加減

正の数・負の数をひくことは、その数の符号を変えることと同じです。

3つ以上の数の加減は、加法だけの式になおして、正の項どうし、負の項どうしをまとめて計算します。 または、かっこのない式になおして、正の項どうし、負の項どうしをまとめて計算します。

例）(-5) - (-6) + (-2) + (+3) = -5 + 6 + -2 + 3 = +9 - 7 = +2

加法の交換法則

a + b = b + a

というように加法は交換法則が成立します。 たす数とたされる数を入れかえても、和は同じになります。

加法の結合法則

(a + b) + c = a + (b + c)

というように加法は結合法則が成立します。 前の2数を先に計算しても、うしろの2数を先に計算しても、和は同じになります。

乗法と除法

かけ算のことを乗法（じょうほう）といいます。二つの数に対してそれをかけ合わせて第三の数（積）を求めます。 除法（じょほう）はわり算で、二つの数に対して一方の数から他方の数をわった第三の数を求めることをいいます。

乗法

乗法の結果を積（せき）といい乗法は、同符号の2数の積の場合は絶対値の積に+をつけ、異符号の2数の積の場合は絶対値の積に-をつけます。

例1) (-2) × (-3) = +(2 × 3) = +6

例2) (-3) × (+5) = -(3 × 5) = -15

3つ以上の数の乗法

3つ以上の数の乗法は、負の数が偶数個の場合は絶対値の積に+をつけ、負の数が奇数個の場合は絶対値の積に-をつけます。

例) (-2) × (+1) × (-3) × (-4) は負の数が3個で奇数なので絶対値の積に-をつけます。
(-2) × (+1) × (-3) × (-4) = -(2 × 1 × 3 × 4) = -24

累乗

同じ数をいくつかかけ合わせたものを、その数の累乗（るいじょう）といいます。 累乗のかけ合わせた個数を示す右肩の小さい数を指数（しすう）または累乗の指数といいます。

たとえば、2×2×2と、2を3個かけ合わせる場合は、2³のように書きます。右肩の小さい3の部分が指数です。

乗除の混じった計算

正の数・負の数でわることは、その数の逆数をことと同じです。つまり除法は逆数にすることで乗法になおせます。

乗法と除法の混じった計算は、除法の部分を乗法になおし、乗法だけの式にして計算します。

例）(+6) ÷ (-3) = (+6) × 1 3 = - (6 × 1 3 ) = -2

四則の混じった計算

四則の混じった計算は、累乗・かっこの中　→　乗法・除法　→　加法・減法　の順に計算します。 かっこのある計算では、分配法則が利用できます。

四則

加法、減法、乗法、除法をまとめて四則といいます。

分配法則

分配法則は、かっこのある式を以下のように展開することができるという法則です。

(a + b) × c = a × c + b × c

a × (b + c) = a × b + a × c

(a - b) × c = a × c - b × c

a × (b - c) = a × b - a × c

四則の混じった計算の例

四則の混じった計算の例です。例3では分配法則を使用しています。

例1）(-6) × 2 - 18 ÷ (-3) = (-12) - (-6) = -(12 - 6) = -6

例2）-1.2 - {(-2)² - 2 × (0.5 - 1.4)} = -1.2 {4 - 2 × (-0.9)} = -1.2 - {4 - (-1.8)} = -1.2 - 5.8 = -7

例3）26 - ( 1 7 - 1 3 ) × 42 = 26 - ( 1 7 × 42 - 1 3 × 42) = 26 - (6 - 14) = 26 - (-8) = 34

正の数・負の数の利用

正の数・負の数を利用してみましょう。

平均

平均は、いくつかの数量を、等しい大きさになるように鳴らしたものです。 一般的に「(平均) = (合計) ÷ (個数)」で求めます。 この平均を基準の量との差を正の数・負の数を用いて表し、平均を求めるができます。

(平均) = (基準の量) + (差の平均)

基準の量を仮の平均といいます。

文字と式

数式に文字を使うことで、1つの数式でいろいろな場面に対応できます。 同じ計算を何度もする必要がなくなって、とても便利です。

文字式とは

文字を使って表せる式を文字式といいます。

文字式の例

たとえば、以下のように文字式が作れます。

• 100円の品物a個の代金は、100×a（円）
• 長さ x cmのテープ10本分の長さの合計は、x×10（cm）
• 分速 60 mで b m歩いた時にかかる時間は、b÷60（分）

文字式の立て方がわからないときは、文字を数字に置き換えて考えます。

文字の式のルール

文字式はきまりにしたがって、×や÷の記号を省いて書きます。ただし、たし算の＋、引き算のーは、はぶけないので注意してください。

かけ算の表し方

かけ算は次のように表します。文字を使うと×と÷がはぶけて、すっきり表せます。

1. 乗法の記号×をはぶく。 50×a＝50a
2. 数と文字の積では、数を先に書く。　a×4＝4a
3. 同じ文字の積は、累乗の形で書く。　a×a×a＝a³
4. 文字と文字の積では、アルファベット順に書く。　b×a＝ab
5. 1をはぶく。　1×a＝a、(-1)×b＝-b

たとえば、y×x×x×z×5を文字式の表し方にしたがって書くと、5x²yzになります。

わり算の表し方

除法の記号÷を使わず、分数の形で書く。

a÷b＝ a b

たとえば、(x＋y)÷3を文字式の表し方にしたがって書くと、 x＋y 3 になります。

式の値

文字式の文字にはいろいろな数をあてはめられるから、1つの式でいくつもの計算ができます。 1個の値段が代わったときの代金の合計を計算することもできます。

代入

文字を数に置き換えることを、文字に数を代入（だいにゅう）するといいます。 そして代入して求めた結果を式の値といいます。

例として、x＝5のときの式8x＋1の値を求めてみます。

8x＋1＝8×5＋1だから、
8x＋1＝8×5＋1＝40＋1＝41

よって、x=5のときの式8x＋1の値は41

もう1つ例として、x＝-2のときの式x²の値を求めてみます。

x²＝(-2)²＝4

よって、x＝-2のときの式x²の値は4

項と係数

1つの式の中に同じ文字があるときは、同じ文字どうしでまとめると、たし算、ひき算ができます。

項と係数とは

式を加法（たし算）だけの式になおしたときの、＋で結ばれたそれぞれを項（こう）、文字の項の数の部分を係数（けいすう）といいます。

たとえば、4x-2y+7は、4x + (-2y) + 7と書けますので4xと-2yと7が項です。係数は4xの4が文字xの係数、-2yの-2が文字yの係数です。

なお、数字のない文字が項の場合もx=1×xというように係数1が隠れています。

文字の部分が同じ項をまとめる

文字が同じ項はまとめられます。係数どうしを計算してまとめます。

たとえば、5a+3b-7aという文字式があるとします。これを簡単にしてみます。 5aと-7aは、文字の部分が同じ項なので、係数を計算してまとめることができます。

5a＋3b－7a
＝ 5a－7a ＋ 3b ・・・文字がaの項をまとめます。
＝ (5－7)a ＋ 3b ・・・係数を計算します。
＝ －2a ＋ 3b

文字式の加法・減法

同じ文字を含む式は、文字の項と数の項に分けて、たしたりひいたりできます。 同じ文字の項をまとめればすっきりします。

文字式どうしのたし算

文字式のたし算ひき算では、まずかっこを外し、項を並べ替えます。

3x+1+(2x+5)
＝ 3x+1+2x-5
＝ 3x+2x+1-5
＝ 5x-4

かっこのある文字式のひき算

ひき算は、ひく式全体の符号がかわります。

(3x+8)-(2x-5)
＝ 3x+8-2x+5
＝ 3x-2x+8+5
＝ x+13

2. 方程式

問題の条件が複雑で、単純な計算ではすぐに答えが出せないとき、わからない数をxとして方程式をつくると、わからない数をもとめられます。

方程式とは

方程式は、「わからない数」が入った等式です。

たとえば、ある数xを3倍して2を加えたら20になったことを表す等式は、

3x+2=20

このように、わかっていない数を表す文字を含む等式を方程式といい、 わかっていない数を求めることを方程式を解くといいます。

方程式は、文字に特別な値を代入したときだけ成り立ちます。 方程式を成り立たせる文字の値（上の式ではx=6）を方程式の解といいます。

等式の性質の利用

文字にいろいろな値を代入して方程式の買いを求めるのは大変です。 等式の性質を使うと、もっとシンプルに解を求めることができます。 以下の4つの等式の性質を使って式をx＝〇の形にしましょう。

1. 等式の両辺に同じ数をたしても、等式が成り立つ。

   A＝Bならば、A＋C＝B＋C

   x - 5 = 3　→　x - 5 + 5 = 3 + 5　→　x = 8

2. 等式の両辺から同じ数をひいても、等式が成り立つ。

   A＝Bならば、A - C＝B - C

   x + 5 = 3　→　x + 5 - 5 = 3 - 5　→　x = -2

3. 等式の両辺に同じ数をかけても、等式が成り立つ。

   A＝Bならば、A × C＝B × C

   x ÷ 5 = 3　→　x ÷ 5 × 5 = 3 × 5　→　x = 20

4. 等式の両辺を同じ数でわっても、等式が成り立つ。

   A＝Bならば、A ÷ C＝B ÷ C

   2x = 30　→　2x ÷ 2 ＝ 30 ÷ 2　→　x = 15

このように、等式の性質を使うと、左辺をxだけの式にして、方程式を解くことができます。

3. 関数とグラフ

小学校で習う比例や反比例など、関数がわかると、2つの数量の関係がとらえやすくなります。

関数とは

関数は、ともなって変わる2つの数量の関係を表します。

たとえば、空の水そうに、1分間に3㎝ずつ水位が上がるように水を入れます。 x分後の水位をy㎝とすると、xとｙの関係は下の表のようになります。

x	0	1	2	3	…
y	0	3	6	9	…

このように、ともなって変わる2つの数量x、yがあって、 xの値を決めるとyの値が1つだけきまるときyはxの関数であるといいます。

上の例をxとyの関係を式で表すと、y=3xとなっています。

なお、年齢と体重のように一方が決まっても他方がそれにともなって変わらないものは、関数ではありません。

比例の関係

小学校で習った比例を、関数の考え方を使って見ていくと、 xとyの関係が、y＝定数×xのとき、yはxに比例しているといいます。 比例の関係は、ふだんの生活でもたくさん登場します。

比例はxとyが同じ倍率で変化する

1個100円の品物をx個買ったときの代金をy円とすると、xが2倍なら、yも2倍、xが100倍なら、yも100倍、どこまでも同じ倍率になります。

x（個）	0	1	2	3	4	…
y（円）	0	100	200	300	400	…

個数xが2倍、3倍、・・・になると、代金yも2倍、3倍、・・・になっています。 このとき、yはxに比例するといいます。

yがxに比例するとき、y＝axと表されます。 aを比例定数といいます。 上の表で、y＝100×xになっているから、代金yは個数xに比例していて比例定数は100です。

xやyのようにいろいろな値をとる文字を変数といいます。

4. 平面図形

平面図形についての基本的な内容についてまとめていきます。

図形の表し方

図形や角や辺、平行や垂直などは、記号を使って短く表すことができます。

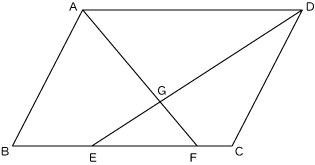
上の図のそれぞれを以下のように記号を使って表すことができます。

• 三角形ABF　…　△ABF
• 平行四辺形ABCD　…　□ABCD
• 角ABC　…　∠ABC
• 辺ADと辺BCが平行　…　AD||BC
• 辺AFと辺DEが垂直　…　AF⊥DE
• 辺ADと辺BCの長さが等しい　…　AD＝BC
• 角ABCと角ADCの大きさが等しい　…　∠ABC＝∠ADC
• 三角形ABCと三角形CDAの面積が等しい　…　△ABC＝△CDA
• 角Bが80°　…　∠B＝80°
• 辺ADが6cm　…　AD＝6cm

図に書き込む記号は次の通りです。

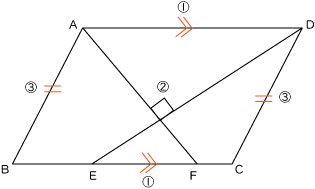
• ①は「辺ADと辺BCが平行」を表します。
• ②は「辺AFと辺DEが垂直」を表します。
• ③は「辺ABと辺DCの長さが等しい」を表します。

平行移動・対称移動

形と大きさを変えないで、図形をほかの位置に動かすことを、移動するといいます。

平行移動

図形を一定方向に一定の距離ずらした移動を、 平行移動といいます。

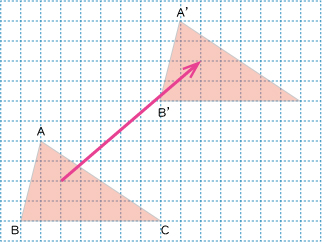
上の図の△ABCと△ABCを平行移動させた△A'B'C'について、A→A'、B→B'、C→C'の移動した方向と距離は同じです。

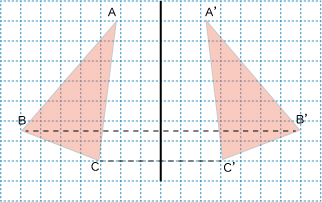
対称移動

図形を1本の直線で折り返す移動を、 対称移動といいます。 このときに折り目とした直線を、 対称の軸といいます。

5. 空間図形

空間図形についての基本的な内容についてまとめていきます。

いろいろな立体

立体を知るために、まずは立体を分けてみます。

角柱・円柱

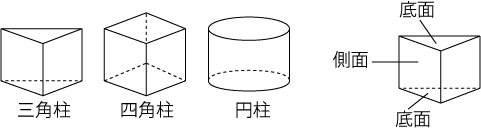
角柱は、底面の形によって、三角柱、四角柱、・・・といいます。 底面が正三角形、正方形、・・・で、側面がすべて合同な長方形のとき、正三角柱、正四角柱、・・・といいます。

角錐・円錐

角錐（かくすい）も角柱と同じように、底面の形で名称が決まります。 底面が正三角形、正方形、・・・で、側面がすべて合同な二等辺三角形のとき、正三角錐、正四角錐、・・・といいます。

多面体

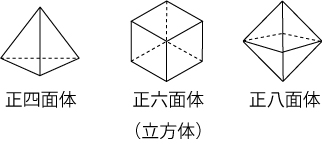
平面だけで囲まれた立体を多面体（ためんたい）といい、 面の数によって四面体、五面体、といいます。 正四面体、正六面体（立方体）、正八面体、正十二面体、正二十面体の5つを正多面体といいます。 正多面体は、すべての面が合同な多角形で、どの頂点にも同じ数だけ面が集まり、へこみのない多面体です。

6. データの活用

私たちの身の回りのことがらを対象として、集団の傾向を調べたり、個人の集団における位置をつかんだりする方法を見ていきます。 また、あることがらの起こりやすさを数値で表したり、全体の一部を取り出して全体の傾向を推定したりといったことも見ていきます。

データの整理

データを整理して表をまとめると、データの特徴がわかるようになります。

データの整理とは

以下のようなデータの分布を、共通点をさがしながら整理すると、特徴がつかめてきます。

1組の生徒が予習に費やした時間（分）：27、44、32、42、31、39、51、43、42、43、42、33、47、29、48、32、44、37、40、3

度数分布表とは

データを下の表のように整理したものを、 度数分布表（どすうぶんぷひょう） といいます。

予習に費やした時間

階級（分）	度数（人）
以上　未満 25 ～ 30	2
30 ～ 35	4
35 ～ 40	3
40 ～ 45	8
45 ～ 50	2
50 ～ 55	1
合計	20

1つ1つの区間を階級（かいきゅう）といい、 区間の幅を階級幅（かいきゅうはば）、 それぞれの階級に入る記録の個数を、その階級の度数（どすう）といいます。 それぞれの階級のまん中の値を階級値（かいきゅうち）といいます。

上の度数分布表で、 階級の幅は30-25=5（分）、 30分以上35分未満の階級の度数は4（人）、 階級値は(35+30)÷2=32.5（分）、 度数の最も多い階級は40分以上45分未満 です。

もっと知識を広げるための参考

• テクノロジ系

  情報処理試験対策用のサイトオリジナル教科書をテーマにテクノロジ系の知識をまとめています。

更新履歴

• 2023/12/31 文字式の加法・減法について追記しました。
• 2023/12/25 データの活用について追記しました。
• 2023/12/7 空間図形について追記しました。
• 2023/11/28 平行移動・対称移動について追記しました。
• 2023/11/24 記事をUPしました。

戻る